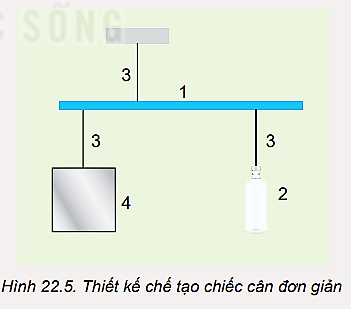
Chế tạo một chiếc cân thăng bằng đơn giản bằng các vật liệu dễ tìm (Hình 22.5):

1. Một thanh thước gỗ có vạch chia.

2. Một chai nước 500 ml.

3. Các dây treo.

4. Vật cần treo.

Lời giải:

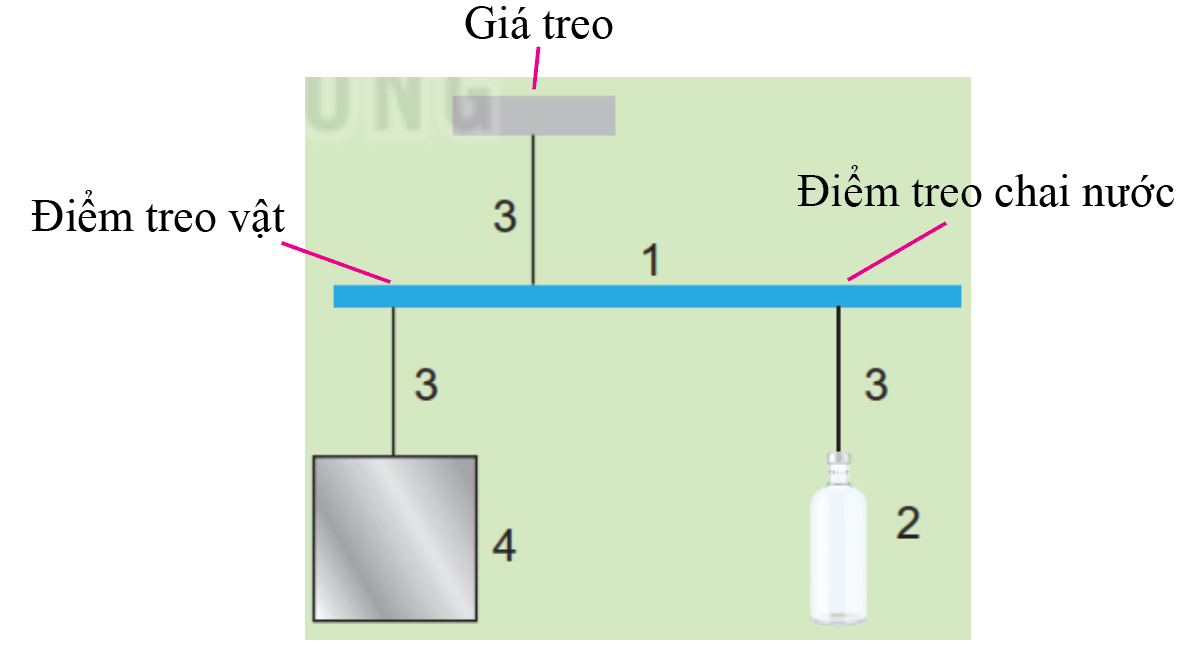
Chế tạo chiếc cân như hình trên.

- Buộc chai nước vào một sợi dây treo, sau đó buộc vào thanh thước gỗ màu xanh (sao cho có

thể dễ dàng di chuyển điểm treo chai nước để chai nước ở các vị trí khác nhau).

- Buộc hệ vào giá treo phía trên.

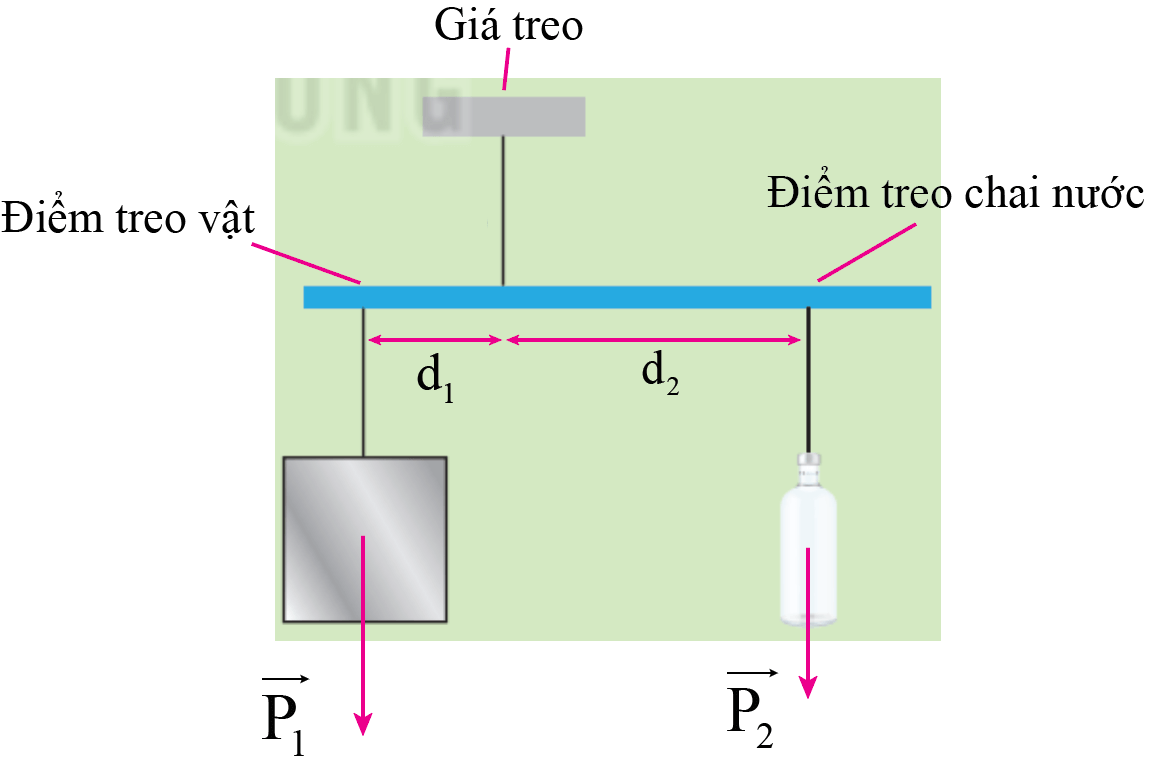
Lí thuyết: khi treo các vật vào cân thì cân sẽ bị lệch, để cân thăng bằng sẽ phải di chuyển điểm

treo của chai nước cho đến khi thanh thước nằm ngang.

Tính toán:

- Có thể tích chai nước, từ đó tính được khối lượng của chai nước ta hoàn toàn có thể tính

được trọng lượng của nó là P₂.

- Đọc khoảng cách từ giá của các lực $\overrightarrow{P_1}; \overrightarrow{P_2}$đến trục quay.

- Sử dụng công thức: $\frac{P_1}{P_2}=\frac{d_2}{d_1} \Rightarrow P_1=\frac{d_2}{d_1}.P_2$=> m₂ = ...